Shingoの数学ノート

プログラミングと機械学習のメモ

統計学と線形回帰分析2(仮説検定とp値)

日付：    カテゴリ： データ分析

前回の続きです。まだ見ていない方はそちらから見てください。前回と同様、標本から求められた偏回帰係数を$\hat\beta_i$、母集団の偏回帰係数を$\beta_i$としています。


仮説検定とp値 概要

よく言葉は耳にするけど、解釈しようとするとなかなか難しいのがp値です。まずp値を知る前に、仮説検定について少しだけ説明します。


仮説検定とは、母集団のある性質を標本の統計量を使って検証をする手法です。線形回帰分析のt検定と呼ばれる仮説検定では、ある説明変数が目的変数に対して影響をもっているかを検定します。


<仮説検定の手順>
  1. 母集団に関する棄却したい仮説(帰無仮説)と主張したい仮説(対立仮説)を設定します。線形回帰分析では帰無仮説を「説明変数が目的変数に対して影響を持っていない」=「母集団の偏回帰係数が0」、つまり「$\beta_i=0$」と仮定し、対立仮説を「$\beta_i \ne 0$」と仮定します。

    2. 仮説検定の説明1

  2. 帰無仮説が成り立っていると仮定したときに、標本から得た統計量がどのくらいの確率で起こるかを求めます。この確率をp値と呼びます。線形回帰分析では、「$\beta_i=0$」を仮定したとき、今回計算した$\hat\beta_i$がどのくらいの確率で起こるかを計算します。計算については次の章で解説します。

    3. 仮説検定の説明2

  3. あらかじめどれくらいの確率で起こった場合に帰無仮説を棄却するかを決めておき(この閾値を有意水準と呼ぶ)、p値がそれを下回っていたら帰無仮説がそもそも成り立っていなかったと判断し、帰無仮説を棄却して対立仮説を採択します。例えば線形回帰分析で有意水準を0.05に設定しておいた場合、p値が0.05を下回ったら「説明変数が目的変数に対して影響を持っていない」という仮説を棄却し、「影響を持っている」可能性が高いと判断します。

    4. 仮説検定の説明3


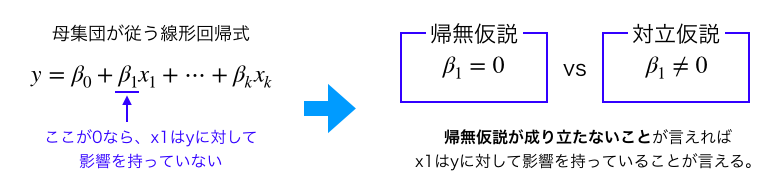
この検定によって帰無仮説を棄却したとき、その仮説は「統計的に有意である」と言います。


線形回帰分析でのp値の計算方法

では実際に線形回帰分析のp値を計算してみましょう。


帰無仮説「$\beta_i=0$」を仮定したとき、今回の標本から求められた$\hat{\beta}_i$はどのくらいの確率であり得るのかを求めます。

実は、$\beta=0$の条件の元では、以下の式が自由度$(n-k)$のt分布に従うことが知られています。これをt値と呼びます。

\[ t=\frac{\hat{\beta}_i}{std\_err} \]

なお、$std\_err$は$\hat{\beta}_i$の(不偏)標準偏差であり、標準誤差と呼ばれます。標準誤差が大きいほど$\hat{\beta}_i$のばらつきが大きくなります。

2020/09/02追記：t値の証明に関するブログをアップロードしました。数学に自信のある方はご覧ください。

t値を使用することにより、今回の確率はどの程度であるのかを算出することができます。ちなみに、自由度$n$のt分布は標準正規分布を自由度$n$の$\chi^2$分布で割った分布であり、以下のような分布になっています。

import scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(-5,5,0.1)
plt.plot(x,stats.t.pdf(x=x, df=2),label="t dim:2",c="blue")
plt.plot(x,stats.t.pdf(x=x, df=5),label="t dim:5",c="green")
plt.plot(x,stats.t.pdf(x=x, df=30),label="t dim:30",c="red")
plt.plot(x,stats.norm.pdf(x=x),label="norm",c="gray")
plt.legend()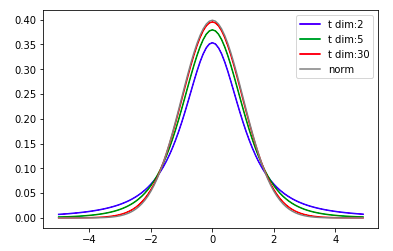
結果
t分布

t分布の自由度を大きくすると、正規分布に従います。


また、$X$を自由度$(n-k)$に従うt分布としたとき、p値は以下のようになります。

\[ p=P(|X|>t|\beta=0) \]

p値は帰無仮説「$\beta_i=0$」を仮定したとき、今回のt値はどれくらいあり得ないかという確率を表しています。もしt値が2、自由度が2であった場合、次のグレーの部分の確率がp値になります。

import scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(-5,5,0.1)
y=stats.t.pdf(x=x, df=2)
plt.plot(x,y,label="t dim:2",c="blue")
plt.fill_between(x,y,0,x<=-2 ,facecolor='gray',alpha=0.5)
plt.fill_between(x,y,0,x>=2 ,facecolor='gray',alpha=0.5)
plt.legend()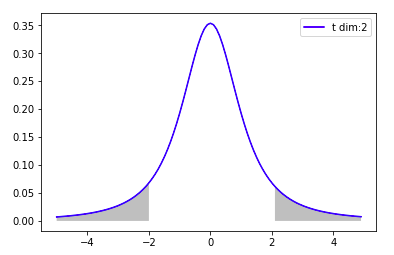
t分布2

p値の実際の計算

では最後に、Boston House Priceのデータのp値の計算をしていきましょう。 今回は変数「INDUS」のp値を求めていきます。(注：前回のブログのコードを実行している状態で以下を実行してください。)

var="INDUS"
n,k=X.shape
print("データ数:",n,"、説明変数の数:",k)
beta=result.params[var]
print("beta:",beta)
std_err=result.bse[var]
print("std_err:",std_err)
t=beta/std_err
print("t値:",t)
p=result.pvalues[var]
print("p値:",p)
x=np.arange(-5,5,0.1)
y=stats.t.pdf(x=x, df=n-k)
plt.plot(x,y,label="t dim:{}".format(n-k),c="blue")
plt.fill_between(x,y,0,x<=-abs(t) ,facecolor='gray',alpha=0.5)
plt.fill_between(x,y,0,x>=abs(t) ,facecolor='gray',alpha=0.5)
plt.legend()
結果 
データ数: 506 、説明変数の数: 13
beta: 0.02055862636706962
std_err: 0.061495688952085036
t値: 0.3343100421736567
p値: 0.7382880714047482
t分布3

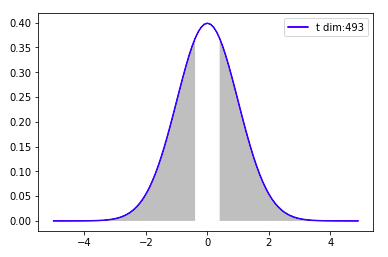
グレーの部分の確率がp値です(0.73)。これほどp値が高いのでは$\beta=0$ではないと結論づけるは難しいですね。


まとめ

  • 仮説検定とは、母集団のある性質を標本の統計量を使って検証をする手法である。
  • 線形回帰では、説明変数が目的変数に対して影響を持っているかどうかを調べる際、帰無仮説を「$\beta_i=0$」としてt検定を実施する。
  • 帰無仮説「$\beta_i=0$」を仮定したとき、今回のデータから得られた$\hat{\beta}_i$はどれくらいの確率なのかを表したのがp値である。

参考文献

1. 統計WEB 重回帰分析 リンク
2. 東京大学教養学部統計学教室 編. 統計学入門(2010,第30版). p175-192. 東京大学出版会
3. 蓑谷 千凰彦 著. 線形回帰分析(2015). 朝倉書店

Comment Box is loading comments...