Shingoの数学ノート

教師あり学習の目的〜解釈と予測〜

日付： 2021-10-31 カテゴリ：データ分析

教師あり学習の目的〜解釈と予測〜

今回のテーマは教師あり学習の目的についてです。

教師あり学習の分析の目的は大きく分けて、解釈と予測の2種類があります。

これらは同じ手法を使う場合が多いですが、見るべき数値や精度の検証方法、期待する成果などが大きく異なっています。

これらの違いを知ることで、今求められている分析は何なのかを理解することができるでしょう。

ということで、今回は以下のデータを使って解釈、予測の例を見ていきます。

実際のコードはこちらを参考にしてください。

データ説明

Boston House Priceのデータ

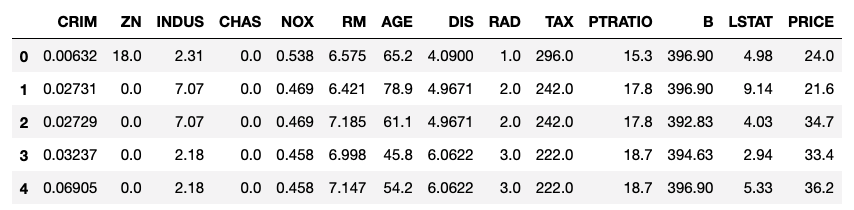
変数説明

変数	説明
CRIM	町別の犯罪率
ZN	25,000平方フィートを超える区画に分類される住宅地の割合
CRIM	町別の犯罪率
INDUS	町別の非小売業の割合
CRIM	町別の犯罪率
NOX	一酸化窒素濃度（parts per 10 million単位）。
RM	1戸当たりの平均部屋数
AGE	1940年より前に建てられた持ち家の割合
DIS	5つあるボストン雇用センターまでの加重距離
RAD	主要高速道路へのアクセス性の指数
TAX	10,000ドル当たりの固定資産税率
B	「1000(Bk - 0.63)」の二乗値。ただし、Bk＝町ごとの黒人の割合
LSTAT	町別の「生徒と先生の比率」
PRICE	住宅価格（1000ドル単位）の中央値。(目的変数)

解釈

教師あり学習の目的の一つ目は、解釈です。

目的変数に対して、どの変数がどれくらい影響しているか、どの変数の組み合わせが目的変数に影響を与えているかをモデルから解釈します。

解釈を目的とするために使用するモデルは線形回帰分析や、決定木などの単純でわかりやすいものが多いです。

解釈(線形回帰)

実際に線形回帰分析で、どの変数が効いているかを出力してみましょう。

以下は、Boston House Priceに対してそのまま線形回帰分析を適用します。

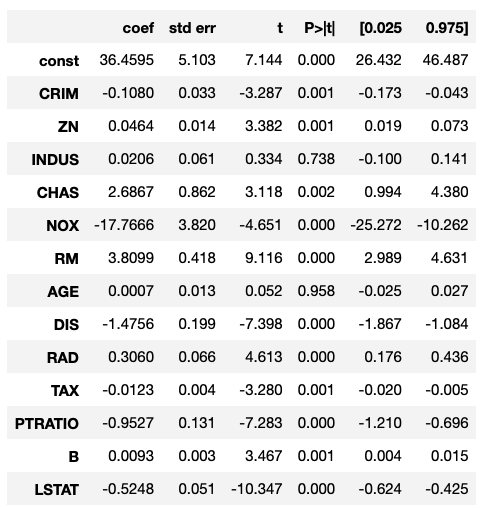
p値などを見て、影響している可能性がある変数などに当たりをつけます。

とはいうものの、偏回帰係数では元の変数のスケールによって変化してしまうため、そのままでは変数同士の比較できません。

そこで、説明変数と目的変数を標準化して線形回帰分析を適用します。

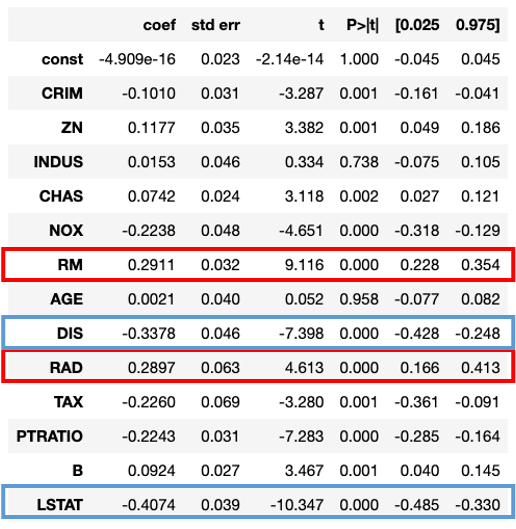
この標準化した偏回帰係数とp値の結果から、以下のことがわかります。

RM(1戸当たりの平均部屋数)やRAD(主要高速道路へのアクセス性の指数)がPRICE(住宅価格)がプラスに影響していそう
LSTAT(低所得者人口の割合)やDIS(5つあるボストン雇用センターまでの加重距離)などがマイナスに影響していそう

(実際の業務では残差や散布図も見てp値や偏回帰係数を判断する必要があります。)

解釈(決定木)

また、決定木を使って目的変数に対して何が効いているのかを可視化することもできます。

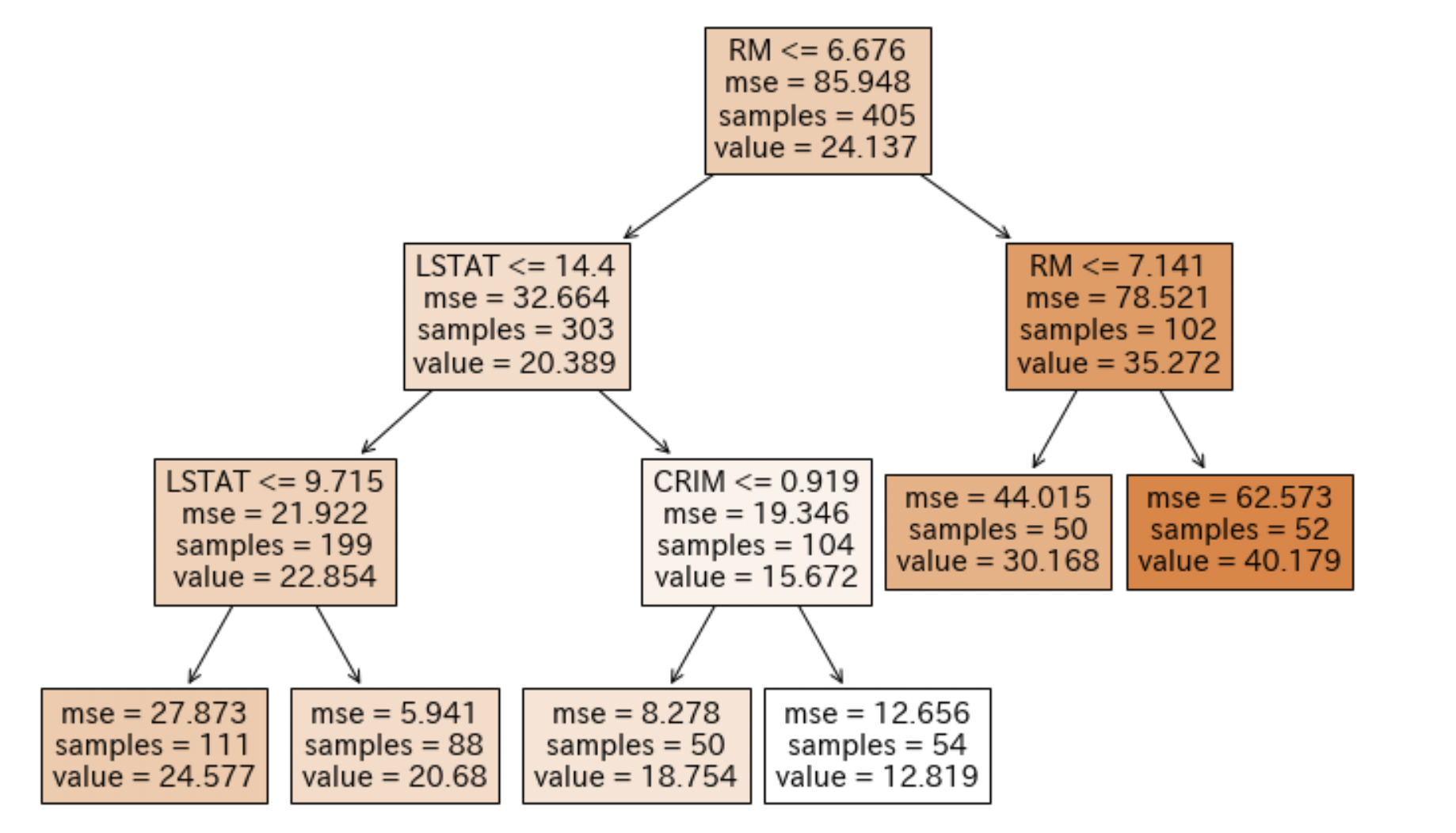
上記の例では、RM(1戸当たりの平均部屋数)が7.141より大きいとPRICEの平均(図のvalue)も大きくなることがわかるかと思います。

とくに、説明変数がカテゴリ値のときは線形回帰で扱うのは難しいので、決定木を使う場合も多いです。

解釈(散布図)

もちろん変数の解釈をするには目的変数との相関も直接見ます。

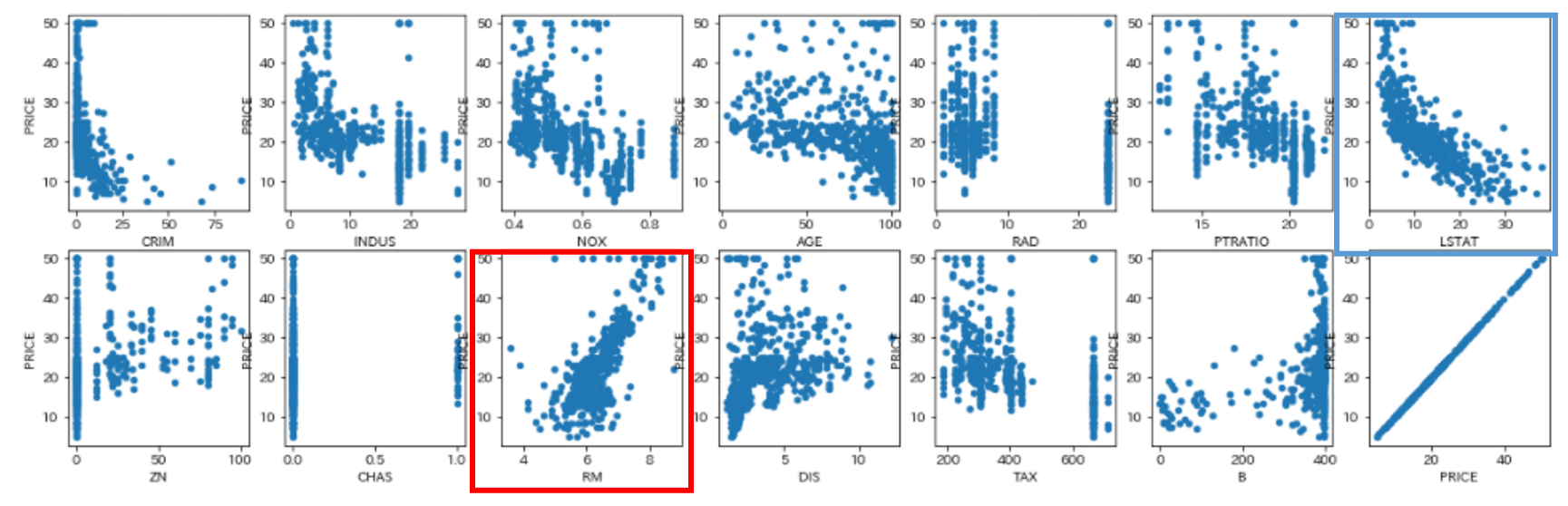
目的変数PRICEに対して、RMが正の、LSTATが負の相関にあることがわかります。

解釈(まとめ)

解釈で大事なのは、以下の通りです。

解釈が妥当か
本当に効いていると言えるのかどうか(仮説検定)
どの程度効いているのかを知る
今ある標本は正しくランダムサンプリングされているか(偏っていないか)

そのため、ぱっと見てわかる、解釈しやすいモデルを使用することが多いです。

また、解釈性を重視する場合、訓練データと検証データを分けずに全体でモデルを作成する場合もよくあります。

予測

教師あり学習の目的の二つ目は、予測です。

予測では、精度や未知データの当てはまりを第一に考えます。

したがって、訓練データと検証データに必ず分割して、訓練データで学習を行い、検証データで評価を行う必要があります。

また、予測を行う際は、訓練データと検証データの分け方、評価方法、評価指標、未知のデータと学習するデータが一致しているかなどを気にします。

特に評価方法はK-Foldクロスバリデーションなどを使用します。

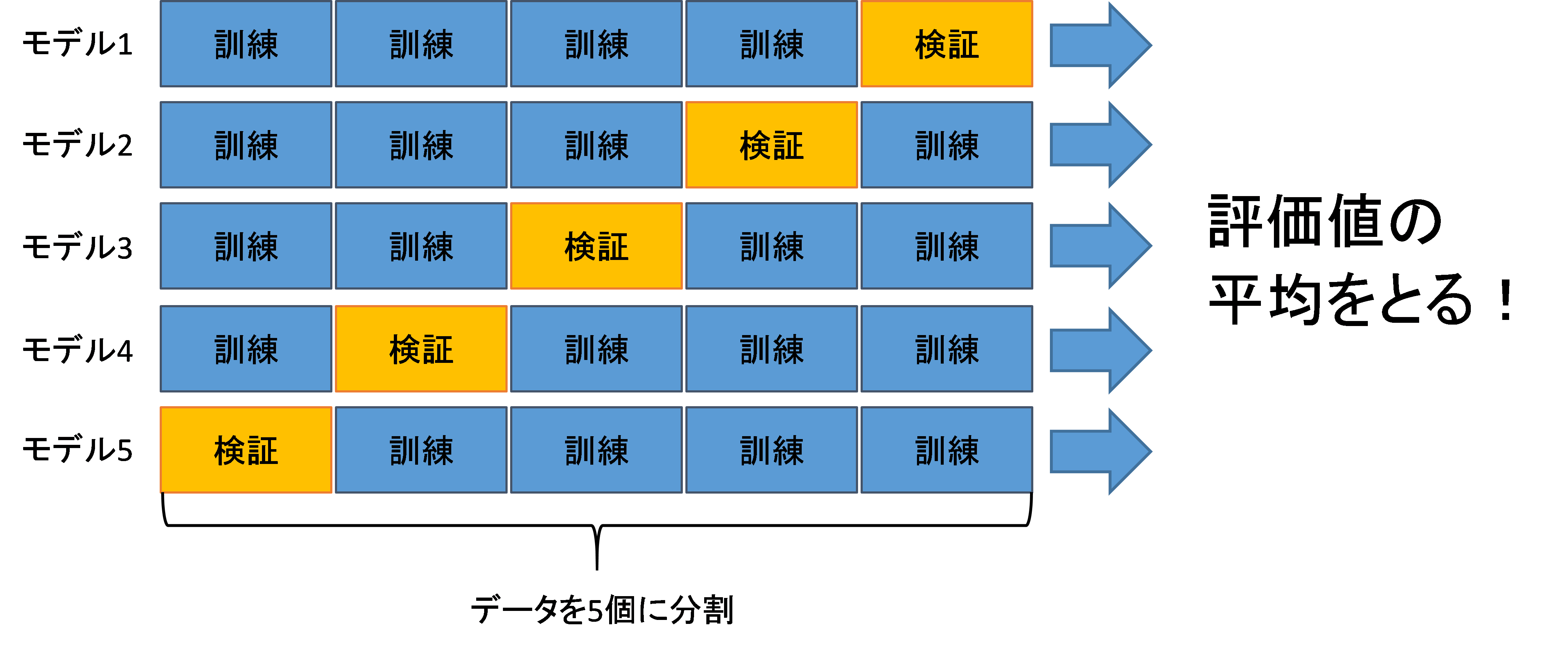
K-foldクロスバリデーション(例えばk=5)とは、データを5個に分割し、4個を訓練するためのデータ、1個を検証するためのデータとして5回回し、検証データの平均や5個のスコアを見て、最終的な精度を出力する方法です。

ランダムに一回分けるよりも評価が安定します。

モデルは、複雑で高精度なモデル(LightGBMなど)を使用する場合が多いですが、解釈の余地も残したい場合は線形回帰や決定木を使うこともあります。

実際に線形回帰と決定木で予測を行うコードはこちらの予測の章を見てください。

予測で大事なのは、以下の通りです。

適切なモデルで適切な精度の検証方法か
その精度は予測対象のデータの当てはまりを考慮できているか
教師データと予測対象のデータは同じ分布か
うまく特徴量エンジニアリングして精度を上げられるか

もちろん、実際の業務では予測とともにどんな変数が効いているかを問われることもありますが、その場合は偏回帰係数や変数重要度を見ましょう。

まとめ

今回は、教師あり学習の分析の目的について、解釈と予測の２つを紹介しました。

分析手法は同じでも、目的によって見るべきポイント、データの使い方などが異なってくるので、今行っている分析は解釈、予測どちらを重視しているのか意識してみると、分析の道筋が立てやすくなると思います。