Shingoの数学ノート
プログラミングと機械学習のメモ
中心極限定理
日付: カテゴリ: データ分析
今回は、中心極限定理について少し書いていこうと思います。
中心極限定理とは
表と裏の出る確率が0.5であるコインがあります。このコインの試行回数$n$を増やせば標本平均$(=\frac{表が出る回数}{試行回数})$は平均$\mu$に近づくことは以前の記事で書きました(大数の法則ですね)。
中心極限定理は、その標本平均はどのように平均に近づくのか、標本平均の分布について言及した定理になります。
正しく書くと、中心極限定理とは、「Xが平均$\mu$(有限)、分散$\sigma^2$(有限)となる確率変数は、いかなる分布でもサンプルサイズを大きくすれば、その標本平均は平均$\mu$、分散$\frac{\sigma^2}{n}$の正規分布に従う」です。実際に試してみましょう。
コイントスと中心極限定理
実際にコイン投げを3回、5回、10回投げたときの標本平均の分布を見てみましょう。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
p3=[]
p5=[]
p10=[]
for i in range(10000):
p3.append(np.random.binomial(n=1,p=0.5,size=3).sum()/3)
p5.append(np.random.binomial(n=1,p=0.5,size=5).sum()/5)
p10.append(np.random.binomial(n=1,p=0.5,size=10).sum()/10)
plt.hist(p3,bins=4)
plt.title("n=3")
plt.show()
plt.hist(p5,bins=6)
plt.title("n=5")
plt.show()
plt.hist(p10,bins=11)
plt.title("n=10")
plt.show()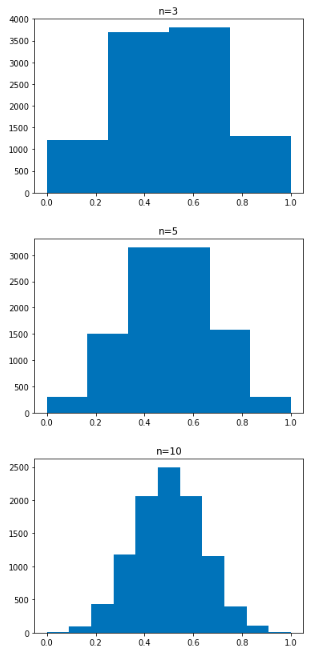
nを大きくするにつれて正規分布に近くなっているのがわかります。
大数の法則と中心極限定理の関係
nを大きくすれば、より正規分布の形に近くなることがわかりました。では、コイントスを10000回したら超きれいな正規分布の形になるに違いない!と いうことで試してみましょう。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
p10000=[]
for i in range(10000):
p10000.append(np.random.binomial(n=1,p=0.5,size=10000).sum()/10000)
plt.xlim([0,1])
plt.hist(p10000,bins=10)
plt.show()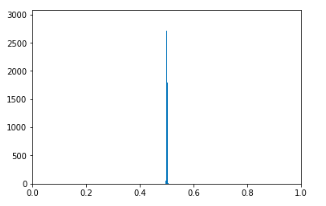
思ってたのと違う…と思う人もいるかもしれません。しかし、中心極限定理をよくみてみると、「分散$\frac{\sigma^2}{n}$」の正規分布に従うので、$n$が大きくなれば分散が小さくなります。だから0.5に近いところで分布が密集しているのです。
さて、勘のいい方はお気づきかもしれませんが、実はこれ、大数の弱法則と全く同じことを言っているのです(大数の弱法則についてはこちらを参照)。つまり、$n$を大きくすれば、標本によるばらつきが少なくなり、標本平均は平均に近づいていくのです。
まとめ
- 中心極限定理とは、標本平均の分布が正規分布になる定理である。
- 標本平均はnを十分大きくすると、分布は平均に密集する。これは大数の弱法則と同義である。