Shingoの数学ノート
プログラミングと機械学習のメモ
SASのproc regで線形回帰
日付: カテゴリ: データ分析
SASで線形回帰
今回は、SASで線形回帰を実施する方法を紹介します。
無料版SASでも試せます。
https://www.sas.com/ja_jp/software/on-demand-for-academics.htmlSASで線形回帰を実施するメリット
現在統計ツールはたくさん出回っており、線形回帰だけならPython、Rといったプログラミングでも可能です。
その中でSASは、残差分析や回帰診断がデフォルトで備わっている、標準偏回帰係数やVIFなどが簡単に出せる、 統計に必要な多くの指標(R^2やAIC)を算出してくれるなど、本格的に分析するのであればSASに軍配が上がるかと思います。
proc regで線形回帰
SASで回帰分析を行うには、proc regとproc hpregがありますが、今回はproc regについて解説していきます。
学習するためのデータと予測を適用するためのデータを用意しておきます。
data BASEBALL;
set sashelp.BASEBALL;
run;
data BASEBALL_test;
set sashelp.BASEBALL;
if _n_ < 30 then output;
drop logSalary;
run;まずはproc regで線形回帰を実施します。
proc reg data=BASEBALL plots=all outest=estb;
model logSalary = natbat
nhits
nhome
nruns
yrmajor
nouts
nassts
nerror/STB VIF;
run;proc regでは、plots=allを選択することで、多くのグラフを算出できます。
outest=で線形回帰のパラメータをSAS データセットに保存します。
model <目的変数>=<説明変数> で線形回帰の式を定義します。
オプションの「STB」は標準偏回帰係数、「VIF」は分散拡大の表示を表します。
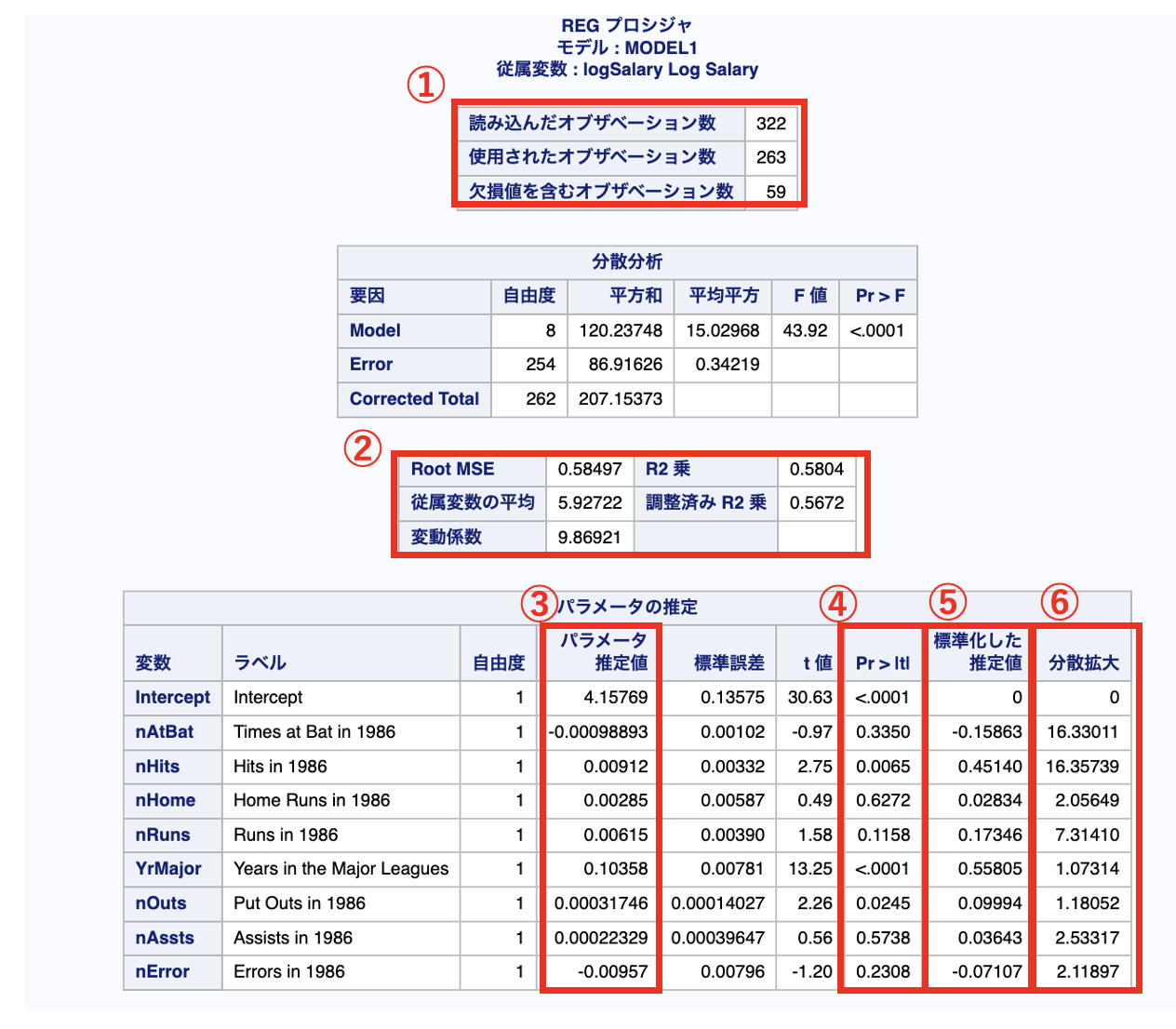
読み込んだ行数、線形回帰で使用された行数、欠損値が含まれている行数を出力します。 SASでは、説明変数または目的変数に欠損値が一つでも含まれていると線形回帰に使用されません。 この行数をみて、想定通り行が使われているかを判断します。
決定係数や調整済み決定係数などの当てはまりのよさ確認できます。
パラメータ推定値
偏回帰係数の値を表示します。ここでは、1単位あたりどの程度の影響があるかを判断します。
P値
偏回帰係数のP値を計算します。
-
標準化した推定値
偏回帰係数ではスケールによって値が変化するため、他の偏回帰係数と比較することができません。そのため、説明変数と目的変数を標準化してから影響の大きさを比較します。 今回ではlogSalaryに対して、他の変数と比較してYrMajorの影響が高そうであることがわかります。
-
分散拡大
VIFとも呼ばれ、一般に10以上あると多重共線性が疑われます。 今回の例ではnAtBatやnHitsのVIFが高いため、それらの変数のどちらかを減らすなどの対策が必要です。
その他、たくさんグラフが出てきますので、都度確認します。
私がよく確認する点は以下です。
- 外れ値がないか
- 残差が正規分布に近い形か
- 残差の傾向はあるか
proc regで予測
多重共線性は起きていますが、一旦このモデルで予測してみましょう。
proc score data = BASEBALL_test out=BASEBALL_test_predict score=estb type=parms;
var natbat
nhits
nhome
nruns
yrmajor
nouts
nassts
nerror;
run;data=で予測したいデータを指定します。
out=で出力データセット名を指定します。
score=でproc regのoutestで指定したデータセットを指定します。
typeでoutestのどのtypeを使用するかを指定します。基本はparmsで問題ないです。
varステートメントで使用する変数を指定します。proc regで学習したモデルの際の説明変数を入れましょう。
以上で、「BASEBALL_test_predict」に予測値がつきます。
まとめ
今回はSASで線形回帰分析を実行する方法を記載しました。
回帰分析手法にはproc hpregもあるので、書く気力があれば今後はそちらも紹介したいと思っています。