Shingoの数学ノート

最尤推定量の統計的性質

日付： 2020-5-16 カテゴリ：データ分析

はじめに

今回は、最尤推定量について掘り下げていこうと思います。

なお、筆者は統計学についてはかじった程度なので、間違い等あったら指摘していただけると助かります。

最尤推定法とは

まず、最尤推定法について軽く説明します。

最尤推定法は確率分布のパラメータを求める方法の一種で、「ある確率分布(ただしパラメータが不明)があったとして、その確率分布から今あるデータが起こったという事象が起きているという状況から、不明なパラメータはなにであったか」を推定するものです。例を見てみましょう。

あるクラスの生徒の数学の点数は以下のようになっています。

A	B	C	D	E	F	G	H	I	J
87	69	71	99	51	24	26	51	61	57

数学の点数は独立同分布で正規分布にしたがっていることがわかっているとき、正規分布のパラメータである平均と分散はいくつでしょうか？

最尤推定法は、「パラメータをいろいろ変えて今あるデータである確率(連続型確率分布の場合は確率密度関数の値)を出してみて、最も高いものをパラメータの推定量としよう」という考えのもと推定していきます。

当然パラメータは無限の可能性がありいちいち代入していられないので、パラメータを変数とみた関数を考え、これが最大となるパラメータを最尤推定量とします。このパラメータを変数とみた関数を尤度関数といいます。

データの値を$\{x_i\}_{i=1}^n$、正規分布の平均、分散をそれぞれ$\mu$と$\sigma$とおくと、今回の尤度関数Lは以下のようになります。(積で書くことができるのは独立だからです。)

\[ L=f(x_1,\cdots,x_n|\mu,\sigma)=\prod_{i=1}^n\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x_i-\mu)^2}{2\sigma^2}) \]

尤度関数の最大値を考えるわけですが、積の微分は大変です。そこで、logをとっても値の大小関係は変わらない(=関数が最大となるパラメータは変わらない)ことを利用し、logをとって簡単にしてからその最大値を求めます。尤度関数にlogをとったものを、一般に対数尤度関数と言います

\[ logL = -\frac{n}{2}log(2\pi\sigma^2) - \sum_{i=1}^n\frac{(x_i-\mu)^2}{2\sigma^2} \]

最大値を求めるには、パラメータで偏微分してあげて、0になる点を求めます。ここでは真の値と区別するため、推定する$\mu$と$\sigma^2$を$\hat{\mu}$と$\hat{\sigma^2}$とおきます。

\[ \frac{\partial}{\partial \hat{\mu}}(logL)=- \sum_{i=1}^n\frac{(x_i-\hat{\mu})}{\hat{\sigma^2}}=0 \\ \frac{\partial}{\partial \hat{\sigma^2}}(logL)=-\frac{n}{2\hat{\sigma^2}}+\sum_{i=1}^n\frac{(x_i-\hat{\mu})^2}{2\hat{\sigma^2}^2}=0 \]

これを解くと以下のようになります。

\[ \hat{\mu} = \frac{1}{n}\sum_{i=1}^nx_i=\bar{x} \\ \hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2 \]

したがって、このデータの平均と分散の最尤推定量は以下のように求めることができます。

import numpy as np
a = np.array([87, 69, 71, 99, 51, 24, 26, 51, 61, 57])
mu = sum(a)/len(a)
sigma2 = sum((a-mu)**2)/len(a)
print(mu,sigma2)

結果は平均が59.6、分散が507.44と出ます。

最尤推定量の性質

さて、とりあえずパラメータを推定することができました。機械学習の多くの手法では、最尤推定法によってパラメータを推定することが多いです。しかし、このパラメータの推定量、本当に正しいんでしょうか。今回のブログでは、これを掘り下げていきます。

最尤推定量は不偏推定量であるとは限らない

いきなりネガティブですが、最尤推定量は不偏推定量であるとは限りません。

不偏推定量とは、「推定されたパラメータの(標本を変えることによる)平均は真のパラメータと等しい」という性質です。不偏推定量については以前のブログでも書いているので参考にしてください。

今回の場合、正規分布のパラメータの最尤推定量は、平均は不偏推定量になりますが、分散は不偏推定量になりません。(統計学を学んでいるならば、最尤推定量の分散と不偏分散は異なることに気づくでしょう。)

実際に異なる標本で1000回正規分布の最尤推定量を出してその平均を出してみましょう。今回は平均50、分散900(標準偏差30)の正規分布から10データ取得しています。

import numpy as np
import pandas as pd
mu_lists,sigma2_lists=[],[]
for i in range(1000):
    np.random.seed(i)
    a = np.random.normal(50,30,10)
    mu = sum(a)/len(a)
    sigma2 = sum((a-mu)**2)/len(a)
    mu_lists.append(mu)
    sigma2_lists.append(sigma2)
param_df = pd.DataFrame(zip(mu_lists,sigma2_lists),columns=["mu","sigma2"])
param_df.mean()

結果は、muは49.788432、sigma2は815.737927と出ました。muの値は真の値(50)に近いですが、sigma2(900)は少し遠いですね。

ヒストグラムは以下のようになっています。

import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"]=15,5
param_df.hist()

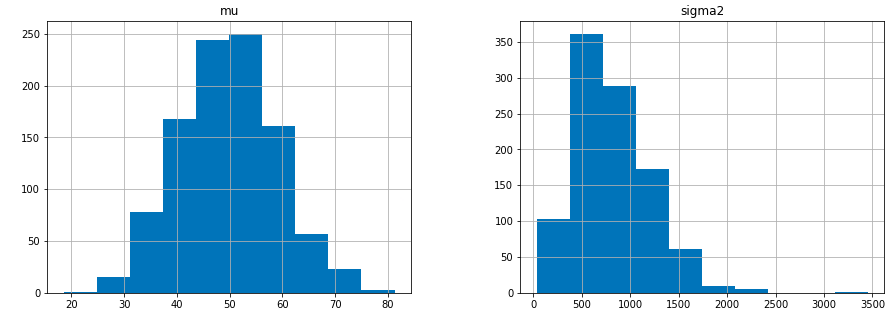
特にsigma2はばらつきが大きいですね。

ちなみに、不偏分散は次の通りです。(最尤推定量の分散にn/(n-1)をかけると不偏分散になります。)

(param_df["sigma2"]*10/9).mean()

結果は906.3754743659838となり、最尤推定量より近い結果になります。

つまり、最尤推定量は必ずしも(不偏推定量的な意味で)いい推定量とは言えないですね。

最尤推定量は(ある正則条件のもと)一致推定量であり、漸近正規性をもつ

じゃあ最尤推定量って統計的に意味のないものなのかと言われると、それは違います。ある正則条件のもと、最尤推定量は一致推定量であり、漸近正規性を持ちます。

これらは漸近理論と呼ばれるもので、データ数nが大きい時になりたつ性質です。

細かくいうと、一致推定量はデータ数nを大きくしたときに真のパラメータに近づく、漸近正規性はデータ数nを大きくしたときに確率分布は正規分布に従う性質を言っています。実際に確かめてみましょう。

まずは、先ほどの最尤推定量を求めるためのデータ数を10000に増やしてヒストグラムを書いてみます。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
mu_lists,sigma2_lists=[],[]
for i in range(1000):
    np.random.seed(i)
    a = np.random.normal(50,30,10000)
    mu = sum(a)/len(a)
    sigma2 = sum((a-mu)**2)/len(a)
    mu_lists.append(mu)
    sigma2_lists.append(sigma2)
param_df = pd.DataFrame(zip(mu_lists,sigma2_lists),columns=["mu","sigma2"])
plt.rcParams["figure.figsize"]=15,5
param_df.hist()

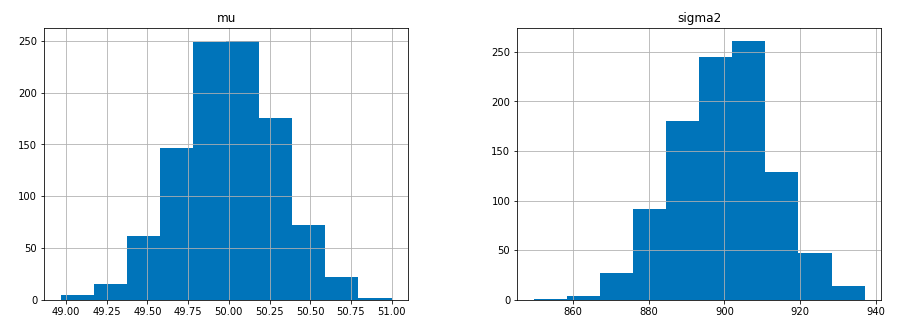
漸近正規性より、ヒストグラムは正規分布になります。また、ここで注目したいのはsigmaです。平均が900あたりになっていますね。

データ数を大きくすれば、最尤推定量は真のパラメータに近くなるのです。

さらに、平均は49から51の間にほとんどあり、分散も860から940の間にあります。

n数を増やすことでさらに間が縮まり、やがては真のパラメータに確率収束するようになります。これが一致推定量の性質になります。

つまり、最尤推定量はデータ数が多いときには性質のいい統計量になることがわかります。

注意！

「ある正則条件のもと」と書きましたが、複雑なモデルであると満たすことが困難になってきます。

正則条件の詳細については参考文献1を参照してください。

正規分布などのよく知られている分布であれば正則条件を満たしますが、混合ガウス分布、潜在ディリクレモデル、隠れマルコフモデル、ニューラルネットワークモデルなどの複雑なモデルでは正則条件に当てはまらなくなってきます。(実際に正則条件が成り立つかは確認していませんが、多分成り立たないと思います。これもいつかブログ書いてみたいです。)このような複雑なモデルで統計的性質をみる場合は工夫が必要です

今回の記事で何が言いたかったかというと、常に最尤推定法によるパラメータ推定はいい性質を持っているとは限らないので、データ数やモデルの複雑さ等を考えて最尤推定法が使えたらいいな、ということです。

まとめ

最尤推定法とは「ある確率分布から今あるデータが起こったという事象が起きている状況から、パラメータはなにであったか」を推定する手法である。
最尤推定法では、「パラメータをいろいろ変えて今あるデータである確率(連続型確率分布の場合は確率密度関数の値)を出してみて、最も高いものをパラメータの推定量としよう」という考えのもと、推定を行う。
最尤推定量は不偏推定量とは限らない。
最尤推定量は(ある正則条件のもと)一致推定量であり、漸近正規性をもつ。

参考文献

野田一雄・宮岡悦良著数理統計学の基礎 p224-p231
Annette J. Dobson 著田中豊・森川敏彦・山中竹春・冨田誠訳一般化線形モデル入門原著第２版