Shingoの数学ノート
プログラミングと機械学習のメモ
統計学と線形回帰分析(母集団と標本)
日付: カテゴリ: データ分析
データサイエンティストの入門として教えられることの多い線形回帰分析。線形回帰分析は統計学や機械学習の基本であり、そしてとても難しい分野であると思います(当時独学で勉強していましたが、本当に意味がわかりませんでした)。今回は、統計学や線形回帰分析について自分が勉強していて難しいなと思った部分を書いていきます。
対象読者
この記事は次の人に向けて書いています。- 実際に線形回帰分析をしたことがある。 or 何かしら線形回帰分析の本やブログを読んだことがある。
- しかし、不偏推定量や一致推定量、p値などの理解が少し怪しい or 初めて聞いた。
- 記述統計と推測統計ってなに?って人
線形回帰分析を全く知らない人は、以下のサイトがわかりやすいので、ご一読ください。
統計WEB 単回帰分析統計WEB 重回帰分析
線形回帰分析とは
はじめに、線形回帰分析って何?っていう人がいるかもしれないので、少しだけ書いておこうと思います。 線形回帰分析とは、連続値のデータ(例えば不動産の価格とか、人数とか)を予測したり、どの変数が効いているかを分析する手法です。以下のような式で予測します。
$y$が予測すべき対象(目的変数)、$x_1,\cdots,x_k$が予測するために使用する変数(説明変数)になります。そして、与えられたデータから$\beta_0,\beta_1,\cdots,\beta_k$(偏回帰係数という)を計算し、未知のデータを当てはめることで$y$を予測できるようになります。
では、とりあえずPythonでの線形回帰分析の実行例を見てみましょう。以下のようなBoston House Priceというデータをロードします。
import pandas as pd
from sklearn.datasets import load_boston
import statsmodels.api as sm
#「boston house price」というデータをロード
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
#boston house priceの上位5件を表示
df[:5]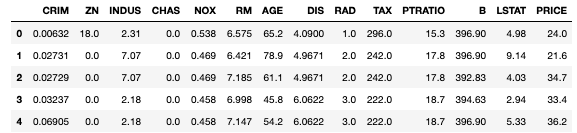
# 変数「CRIM」から「LSTAT」を説明変数として、「PRICE」を予測する
X = df.drop('PRICE',1)
y = boston.target
# add_constantで定数項を挿入
model = sm.OLS(y,sm.add_constant(X))
result = model.fit()
result.summary()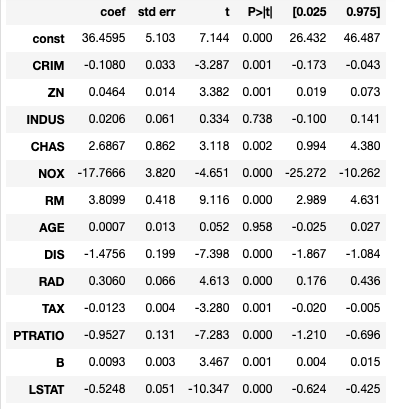
コードを書けば結果が出てきます。ちなみに、「coef」が偏回帰係数、「std_err」が標本誤差、「t」がt値、「P>|t|」がp値、[0.025,0.075]が信頼区間です。なんとなく決定係数が高ければ良いし、回帰係数とかは知っているし、p値は低い方が良いのは知っているが、具体的に何と言われると難しいって人は多いのではないのでしょうか(昔の私はそうでした)。
統計学の考え方
記述統計と推測統計
線形回帰分析においてまず念頭においておきたいのは推測統計という概念です。実際、統計学は大きく分けて記述統計と推測統計に分かれます。
記述統計とは、今あるデータに対して標本平均や標本分散等の要約統計量を算出する統計です。データ分析を行う上でまずやらなければならないことですね。
推測統計とは、今あるデータから母集団のパラメータ(=母数)を推測する統計です。推測統計を考える基本的な考え方として、母集団と標本の概念が必要になってきます。
母集団と標本
さて、推測統計の目的を考えてみましょう。推測統計は、今あるデータについての情報を知りたいのではなく、その先の得られていないデータを含めた全体のデータの統計量を知りたい、というのが目的です。この全体のデータを母集団と言います。そして、今得られたデータは母集団からランダムに抽出されて得られたデータだと仮定します。この抽出されたデータを標本と言います。言い換えれば、ある1標本から母数を求めようとしているのが推測統計なわけですね。
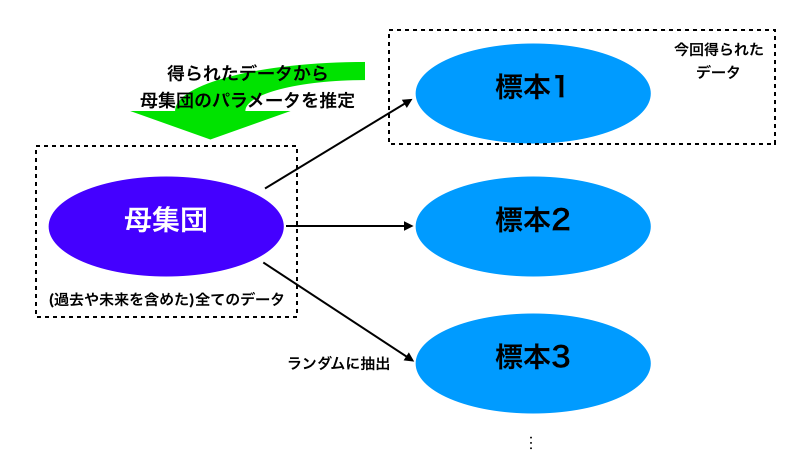
線形回帰分析の例だと、与えられたデータから求められた回帰式はあくまである1標本の回帰式でしかありません。推測統計の概念からいえば、今求めたいのは母集団が従う回帰式になります。当然出てくる疑問として、標本から求めた回帰式は母集団が従う回帰式とどれくらい違うの?とか、標本からの回帰式は母集団の回帰式に近づくの?とかあると思います。これを理論に基づいて証明していったのが線形回帰分析であり、例の結果として出てきたものになります。
線形回帰分析の理論
ここからが本題です。推測統計がある程度わかったところで、線形回帰分析の理論を軽く見てみましょう。なお、標本から求められた偏回帰係数を$\hat{\beta}_i$、母集団が從う回帰式の偏回帰係数を$\beta_i$とします。
偏回帰係数は不偏推定量である
標本偏回帰係数から母集団の偏回帰係数を推測しようとしたとき、当然のことながら値がずれるので、母集団の偏回帰係数を推定するのにある程度良い性質が必要となります。不偏推定量とは良い性質の一つで、標本から算出された統計量を平均すれば母集団のパラメータになるという性質を持つ統計量のことを言います。
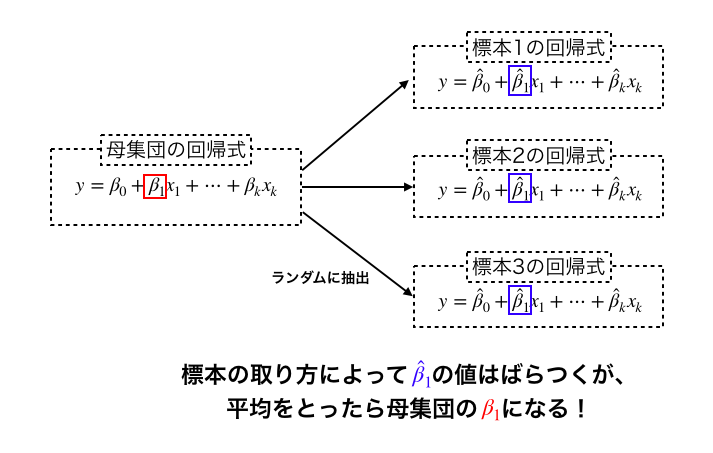
線形回帰分析においては、ある条件を満たせば、偏回帰係数は不偏推定量になります。(詳しく知りたい方はガウス・マルコフの定理を調べてみてください。)つまり、いろんな標本で回帰分析を行えばその偏回帰係数の平均が母集団の偏回帰係数になるということができます。式で書けば以下のようになります。
\[ \beta_i=E[\hat{\beta}_i] \]イメージとしてはこんな感じです。
偏回帰係数は一致推定量である
考え方は不偏推定量似ています。一致推定量とは、サンプルサイズを増やしていけば、標本から算出された統計量が母集団のパラメータに近づくという性質を持つ統計量のことを言います。(正確にいうと、近づくとは確率収束の意味です。ちなみに、標本平均が一致推定量であることと大数の弱法則が成り立つことは同値です。大数の法則や確率収束については前回のブログ記事を参考にしてください。)
線形回帰の偏回帰係数は、一致推定量でもあります。サンプルサイズを大きくしていけば今回のデータで出した偏回帰係数の分散が小さくなり、母集団の偏回帰係数に近づきます。数式で書くと以下のようになります。
イメージとしてはこんな感じです。
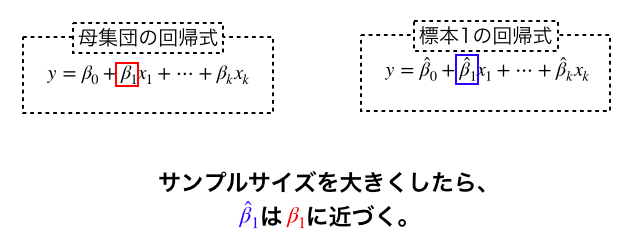
上記から、標本の選ばれ方やサンプルサイズによりますが標本偏回帰係数は母集団の偏回帰係数に様々な意味で近いことがわかります。従って、標本から得られたパラメータをもとに分析結果を解釈していくことが可能になるのです。
仮説検定とp値についても書こうと思っていたのですが、予想以上に長くなってしまったため、次回に回します。
いったんまとめ
- 統計学には記述統計と推測統計がある。
- 線形回帰分析で求められるパラメータは標本からのものであるが、実際に知りたいのは母集団のパラメータである。
- 偏回帰係数は不偏性、一致性をもち、性質のいい推定量である。