Shingoの数学ノート

大数の法則と収束の種類

日付： 2019-06-15 カテゴリ：データ分析

ブログ初投稿になります！今回は統計学の基本である大数の法則について書いていこうと思います。

大数の法則とは

表と裏の出る確率が0.5であるコインがあります。このコインの試行回数を増やしたら標本平均$(=\frac{表が出る回数}{試行回数})$は0.5に近づきそうですよね。この近づきそうっていうのを定式化したのが大数の法則と呼ばれるものです。

上の例を定式化してみます。確率0.5の二項分布に従う確率変数について、$n$が大きくなった時の標本平均を見てみます。

import numpy as np
np.random.seed(1)
p10=np.random.binomial(n=1,p=0.5,size=10).sum()/10
p100=np.random.binomial(n=1,p=0.5,size=100).sum()/100
p1000=np.random.binomial(n=1,p=0.5,size=1000).sum()/1000
p10000=np.random.binomial(n=1,p=0.5,size=10000).sum()/10000
print("n=10 : {}\nn=100 : {}\nn=1000 : {}\nn=10000 : {}".format(p10,p100,p1000,p10000))

結果

n=10    : 0.2
n=100   : 0.54
n=1000  : 0.511
n=10000 : 0.5019

𝑛を大きくすれば確かに0.5に近くなります。当たり前っちゃ当たり前。

色々な分布での大数の法則

上記は二項分布に従う確率変数についての大数の法則を見ましたが、さまざまな分布について大数の法則を見ていきましょう！

ポアソン分布

1日に平均5個不良品が存在する部品があったとすると、1日に不良品が存在する個数の確率はパラメータ5のポアソン分布に従います。これを何日か続けていった場合、その個数の平均は5に近づくでしょうか？試してみましょう。

import numpy as np
np.random.seed(1)
p10=np.random.poisson(5,10).sum()/10
p100=np.random.poisson(5,100).sum()/100
p1000=np.random.poisson(5,1000).sum()/1000
p10000=np.random.poisson(5,10000).sum()/10000
print("n=10 : {}\nn=100 : {}\nn=1000 : {}\nn=10000 : {}".format(p10,p100,p1000,p10000))

結果

n=10    : 4.1
n=100   : 5.15
n=1000  : 4.994
n=10000 : 4.9779

ちゃんと5に近づいてますね。

正規分布

みんな大好き正規分布ですね。平均0、分散1の正規分布から生成された確率変数を何個か生成したら、その標本平均は0に近づくでしょうか？

import numpy as np
np.random.seed(1)
p10=np.random.normal(0,1,10).sum()/10
p100=np.random.normal(0,1,100).sum()/100
p1000=np.random.normal(0,1,1000).sum()/1000
p10000=np.random.normal(0,1,10000).sum()/10000
print("n=10 : {}\nn=100 : {}\nn=1000 : {}\nn=10000 : {}".format(p10,p100,p1000,p10000))

結果

n=10    : -0.09714089080609985
n=100   : 0.07431865897973937
n=1000  : 0.03360117004534288
n=10000 : 0.009015266856491327

標本平均が0に近づき、大数の法則が成り立つことがわかります。

大数の法則が成り立たないケース

さて、今までの例では標本平均が母平均に近づくことを確認しました。では、どんな確率分布でも大数の法則は成り立つのでしょうか？

実は、成り立たない例があります。具体的な例として、コーシー分布があります。コーシー分布とは、標準正規分布同士をわり算した分布です。確率密度関数の形は正規分布に似ていますが、裾が広いのが特徴です。

コーシー分布の確率密度関数 : $f(x)=\frac{1}{\pi(1+x^2)}$

グラフを書くと以下のようになります。正規分布と比べるとかなり裾が広いです。

import matplotlib.pyplot as plt
#関数定義
def normal(x):
    return (np.exp(-x**2/2)) / np.sqrt(2*np.pi)
def cauchy(x):
    return 1/(np.pi*(1+x**2))
#分布作成
x=np.arange(-5,5,0.1)
y_normal=np.vectorize(normal)(x)
y_cauchy=np.vectorize(cauchy)(x)
#描画
splt.plot(x,y_normal,label="normal")
plt.plot(x,y_cauchy,label="cauchy")
plt.legend()

結果

では実際にコーシー分布に従う確率変数の標本平均が0に近づくか見てみましょう。

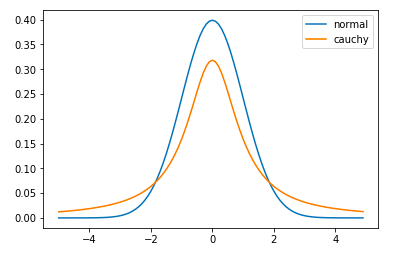
import numpy as np
np.random.seed(1)
p10=np.random.standard_cauchy(size=10).sum()/10
p100=np.random.standard_cauchy(size=100).sum()/100
p1000=np.random.standard_cauchy(size=1000).sum()/1000
p10000=np.random.standard_cauchy(size=10000).sum()/10000
print("n=10 : {}\nn=100 : {}\nn=1000 : {}\nn=10000 : {}".format(p10,p100,p1000,p10000))

結果

n=10    : -0.6742674056116752
n=100   : 0.4863366954564788
n=1000  : -6.369291105541214
n=10000 : 2.640367957638925

全然0に近づいていませんね。これはコーシー分布は裾が長く外れ値を取りやすいために起こります。一般に、大数の法則は平均が有限な確率分布に従う独立同分布な確率変数に対して適用できます。(コーシー分布は実は平均を持ちません。)

収束の種類

ここから難易度が急激に上がります。今まで「近づく」と曖昧に書いていましたが、ここからは数学的に「近づく」を考えていきます。

まず、コイン投げにおける確率変数を考えましょう。結論からかくと以下の様になります。

\[ X_i(\omega)= \begin{cases} 1 \hspace{1cm} (i\mbox{回目で表が出る}) \\ 0 \hspace{1cm} (i\mbox{回目で裏が出る}) \end{cases} \]

上記の$\omega$は標本点と呼ばれ、今回は（表、表、裏、…）等の表裏の組み合わせとして定義します。

次に、大数の法則を数式で書いてみます。$\{X_i\}_{i\in \mathbb{N}}$が独立同分布で$X$の分布に従うとします。$X$の平均が有限のとき、

\[ \begin{equation*} \lim_{n\rightarrow \infty}\frac{X_1(\omega)+X_2(\omega)+\cdots+X_n(\omega)}{n}=E[X]\tag{1} \end{equation*} \]

と書くことができます。

さて、この式は全ての$\omega$について満たしているでしょうか？答えは否です。なぜかと言いますと、もし$\omega'$が全て「表」とした場合、全ての$i$について$X_i(\omega')=1$となるので、以下のようになります。

\begin{equation} \lim_{n\rightarrow \infty}\frac{X_1(\omega')+X_2(\omega')+\cdots+X_n(\omega')}{n}=1 \neq \frac{1}{2} \end{equation}

つまり、$\omega$がどの程度(1)を満たしているかが重要になってきます。実は、どの程度満たすかによって、大数の法則の呼ばれ方が異なってきます。大数の法則には2種類あります！

大数の強法則

まずは強法則から。端的に言ってしまうと、(1)を満たさない$\omega$の集合の確率は0ですよ、というのが強法則です。確率0ってなんだと思われますが、無限回コイン投げを実施して全て表の確率が0であることは計算すればわかります。これを(1)を満たさない$\omega$の集合全体で考えても確率が0になります。式で書くと以下の様になります。

\[ \begin{equation*} P\left(\lim_{n\rightarrow \infty}\frac{X_1(\omega)+X_2(\omega)+\cdots+X_n(\omega)}{n}=E[X]\right)=1 \end{equation*} \]

また、次のようにも書きます。

\[ \begin{equation*} \lim_{n\rightarrow \infty}\frac{X_1(\omega)+X_2(\omega)+\cdots+X_n(\omega)}{n}=E[X] \hspace{3cm} a.s. \end{equation*} \]

「a.s.」はalmost surelyの略で、「ほとんど確実に」という意味になります。この収束の種類を概収束と言ったりします。

大数の弱法則

実は大数の強法則を証明するのって結構難しいんです。ということで、もう少し条件を緩くしたものが大数の弱法則です。定義は以下のようになります。

\[ \begin{equation*} \forall \varepsilon>0 ,\hspace{1cm}\lim_{n\rightarrow \infty}P\left(\left|\frac{X_1(\omega)+X_2(\omega)+\cdots+X_n(\omega)}{n}-E[X]\right|\ge\varepsilon\right)=0 \end{equation*} \]

この式は、$n$を大きくしていくと標本平均は標本によるばらつきが小さくなり、値が期待値に近くなることを表しています。大数の強法則とは$n$を無限にする位置が異なっていますね。この収束を確率収束と言います。

大数の弱法則は中心極限定理と関係があります。もし詳しく知りたければ、こちらも参考にしてください。

まとめ

大数の法則は標本平均が期待値に収束する定理である。
大数の法則は平均を持たない確率変数に対して成り立つとは限らない。
大数の法則には2種類あり、どの程度の$\omega$で(1)が成り立つかで変わってくる。