Shingoの数学ノート

線形回帰分析と最尤推定法

日付： 2020-7-18 カテゴリ：データ分析

はじめに

先日のブログで説明しましたが、最尤推定法は機械学習で多く使用されるパラメータ推定法です。

月並みではありますが、今回は、線形回帰分析のパラメータを最尤推定法で解いてみたいと思います。

線形回帰分析

まずは、線形回帰分析の定義を行います。 $y_i$を目的変数、$x_{ij}$を説明変数とすると、線形回帰分析の式は以下のように表されます。

\[ y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_kx_{ik}+\varepsilon_i \]

ただし、$\varepsilon_i\sim N(0,\sigma^2)$で、独立同分布を仮定します。($\varepsilon_i\sim N(0,\sigma^2)$は、平均0、分散$\sigma^2$の正規分布にしたがっていることを表します。)

これにより、説明変数を定数だとみなすと、$y_i$は、$y_i\sim N(\beta_0+\beta_1x_{i1}+\cdots+\beta_kx_{ik},\sigma^2)$ で、独立な確率変数と見なすことができます。(正確にいうと、$x_{ij}$で条件づけた$y_i$の条件付き確率を考えています。)

線形回帰分析と最尤推定法

さて、$y_i$の確率分布が決まったので、尤度関数を考えてみましょう。

その前に、最尤推定法のおさらいです。

最尤推定法は、「パラメータをいろいろ変えて今あるデータである確率密度関数の値を出してみて、最も高いものをもとのパラメータとしよう」という考えのもと推定していきます。当然パラメータは無限の可能性がありいちいち代入していられないので、パラメータを変数とみた関数を考え、これが最大となるパラメータを最尤推定値とします。このパラメータを変数とみた関数を尤度関数といいます。

ということなので確率密度関数を出しましょう。

パラメータは、偏回帰係数の$\beta_0,\cdots,\beta_k$と、正規分布の分散$\sigma$です。

\[L=f(y_1,\cdots,y_n|\beta_0,\cdots,\beta_k,\sigma)=\prod_{i=1}^n\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_kx_{ik}))^2}{2\sigma^2}) \]

対数尤度関数を考えると、

\[logL = -\frac{n}{2}log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_kx_{ik}))^2\]

ここで、$\beta_0,\cdots,\beta_k$を求めることを考えると、対数尤度関数を最大化するには、以下の式を最小化すれば良いことがわかります。

\[ E=\sum_{i=1}^n(y_i-(\beta_0+\beta_1x_{i1}+\cdots+\beta_kx_{ik}))^2\]

これ、実は最小二乗法と式が同じです。つまり、最小二乗法は、最尤推定法の観点からも妥当なパラメータ推定方法であることがわかります。

最尤推定値を求めてみる

一応$E$を最小化する$\beta_0\cdots\beta_k$も求めておきます。

基本は、全ての$i$について$E$を$\beta_i$で偏微分して0となる$\beta_i$を求めます。ちゃんとやるなら、「偏微分=0」だけでは最小値とは言えず、Eの凸性を議論する必要があります。(下記の「凸関数の最小化」が参考になります。)

http://www2.econ.tohoku.ac.jp/~ksuzuki/teaching/2005/ch5.pdf

ここでは、この証明は省きます。(感覚的には$E$は$\beta_i$に対して2次の多項式で、2次の多項式はは凸関数となるため、凸性を持つことが想像できます。ヘッセ行列を計算してみてもいいでしょう。)

さて、一つずつ$\beta_i$で偏微分するのは面倒臭いので、$\mathbf \beta=\left(\begin{array}{c}\beta_0\\\vdots\\\beta_k\end{array}\right)$、$\mathbf y=\left(\begin{array}{c}y_1\\\vdots\\y_n\end{array}\right)$、$\mathbf X=\left( \begin{array}{cccc} 1 & x_{11} & \cdots & x_{1k} \\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n1} & \cdots & x_{nk} \end{array} \right)$として、一気に計算します。

\[ E=(\mathbf y -\mathbf X\mathbf \beta)^T(\mathbf y -\mathbf X\mathbf \beta)=\mathbf y^T \mathbf y-\mathbf y^T\mathbf X\mathbf \beta-\mathbf \beta^T \mathbf X^T \mathbf y +\mathbf \beta^T \mathbf X^T \mathbf X\mathbf \beta \]

であり、以下の1.2の公式を使用すると、以下となります。

https://qiita.com/AnchorBlues/items/8fe2483a3a72676eb96d

\[ \frac{\partial}{\partial \mathbf\beta}(\mathbf y^T\mathbf X\mathbf \beta)=\frac{\partial}{\partial \mathbf\beta}(\mathbf \beta^T \mathbf X^T \mathbf y)=\mathbf X^T \mathbf y\] \[\frac{\partial}{\partial \mathbf\beta}(\mathbf \beta^T \mathbf X^T \mathbf X\mathbf \beta)=2(\mathbf X^T \mathbf X)\beta \]

したがって、以下が導けます。

\[ \frac{\partial}{\partial \mathbf\beta}E=-2\mathbf X^T \mathbf y+2(\mathbf X^T \mathbf X)\beta=0\] \[\beta=(\mathbf X^T \mathbf X)^{-1}\mathbf X^T\mathbf y \]

これで線形回帰の解析解が求められました。

Pythonによる線形回帰

本当に一致するの？と疑問に思う人もいるかもしれないので、実際に計算してみましょう。

pythonのモジュール(statsmodels使用)

import pandas as pd
from sklearn.datasets import load_boston
import statsmodels.api as sm
#「boston house price」というデータをロード
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
# 変数「CRIM」から「LSTAT」を説明変数として、「PRICE」を予測する
X = df.drop('PRICE',1)
y = boston.target
# add_constantで定数項を挿入
model = sm.OLS(y,sm.add_constant(X))
result = model.fit()
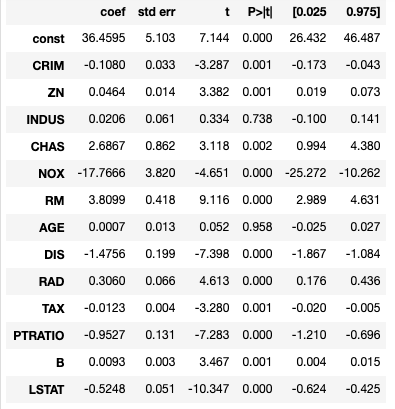
result.summary()

結果：

numpyで先ほど求めた解析解を計算

import numpy as np
X_add = np.array(sm.add_constant(X))
beta = np.linalg.inv((X_add.T @ X_add)) @ X_add.T @ y
pd.Series(beta,index=sm.add_constant(X).columns)

結果：

const      36.459488
CRIM       -0.108011
ZN          0.046420
INDUS       0.020559
CHAS        2.686734
NOX       -17.766611
RM          3.809865
AGE         0.000692
DIS        -1.475567
RAD         0.306049
TAX        -0.012335
PTRATIO    -0.952747
B           0.009312
LSTAT      -0.524758
dtype: float64

coefの部分の結果は一致していますね。

線形回帰のパラメータ推定値の性質

最尤推定値の統計的性質より、一致性と漸近正規性を持ちます。昔のブログで書いた線形回帰分析のパラメータが一致性を持つというのは、パラメータが最尤推定値であることからも証明することができます。

まとめ

線形回帰分析において、最尤推定法によるパラメータ推定と最小二乗法によるパラメータ推定は同じ結果になることがわかります。最小二乗法は最尤推定法の観点からも妥当な推定法であると言えます。

他のポアソン回帰やロジスティック回帰等の一般線形回帰分析も最尤推定法が元になっています。これについても記事をかけたらなと思います。