Shingoの数学ノート

ロジスティック回帰と最尤推定法

日付： 2022-3-27 カテゴリ：データ分析

今回は意外と難しいロジスティック回帰と最尤推定法について解説します。

最尤推定法についてはこちらをご覧ください。

線形回帰分析と最尤推定法についてはこちらをご覧ください。

また、ロジスティック回帰のコードはこちらをご覧ください。

ロジスティック回帰分析

ロジスティック回帰は、0,1の2値を取るデータを分類する問題を解くときに使用するモデルです。

$y_i$を目的変数、$x_{ik}$を説明変数とすると、ロジスティック回帰は以下のように表すことができます。

\begin{align} y_i = \frac{1}{1+\exp(-(\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\cdots+\beta_Kx_{iK}))} \end{align}

また、シグモイド関数を以下の式で定義します。

\begin{align} \sigma(x)=\frac{1}{1+\exp(-x)} \end{align}

シグモイド関数は0から1の値を取り、以下のような関数です。

この関数を使うと、ロジスティック回帰は以下のように書くことができます。

\begin{align} y_i=\sigma(\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\cdots+\beta_Kx_{iK}) \end{align}

シグモイド関数の性質から$y_i$は0から1の値を取るため、0,1の2値を表す確率変数$C_i$を用いて以下のように定義することができます。

\begin{align} P(C_i=1|x_{i1},\cdots,x_{iK})&=y_i\\ P(C_i=0|x_{i1},\cdots,x_{iK})&=1-y_i \end{align}

上記をまとめると、データ$i$の実現値を$t_i$(0か1の2値をとる)として以下のように書くことができます。($t_i$に0と1を入れると上の式になることが確認できます。)

\begin{align} P(C_i=t_i|x_{i1},\cdots,x_{iK})=y_i^{t_i}(1-y_i)^{1-t_i} \end{align}

ロジスティック回帰と最尤推定法

※以下では、文字を太字で書いた場合にはベクトルを表すことにします。(たとえば、$\mathbf{x}=(x_{11},x_{12},\cdots,x_{nK})$を表します。)

この章では、パラメータ$\mathbf{\beta}$を最尤推定法を用いて求めます。

その前に、最尤推定法のおさらいです。

(離散確率分布における)最尤推定法は、「パラメータをいろいろ変えて今あるデータで確率を出してみて、確率が最も高いものをもとのパラメータとしよう」という考えのもと推定していきます。当然パラメータは無限の可能性がありいちいち代入していられないので、パラメータを変数とみた関数を考え、確率が最大となるパラメータを最尤推定値とします。このパラメータを変数とみた関数を尤度関数といいます。

パラメータは$\mathbf{\beta}$であることとデータが独立であることを考えると、尤度関数$L$は以下のように算出することができます。

\begin{align} L &= P(C_0=t_0,\cdots,C_n=t_n|\mathbf{x},\mathbf{\beta})\\ &=\prod_{i=1}^nP(C_i=t_i|\mathbf{x}_i,\mathbf{\beta})\\ &=\prod_{i=1}^ny_i^{t_i}(1-y_i)^{1-t_i} \end{align}

このままでは計算しづらいので、対数を取って対数尤度関数を求めます。(対数は単調増加関数なので、尤度関数が最大となるパラメータは対数を取る前と後で変化することはありません。)

\begin{align} \log L=\sum_{i=1}^n\{t_i\log y_i+(1-t_i)\log (1-y_i)\} \end{align}

パラメータ$\mathbf{\beta}$の最尤推定値を求めるためには、対数尤度関数が最大となる$\mathbf{\beta}$を求めます。

ここで機械学習では、最適化をする場合は損失関数を定義し、最大化ではなく最小化を目指す慣習があります。

従って、対数尤度関数にマイナスをかけて損失関数を定義します。

\begin{align} E=-\sum_{i=1}^n \{t_i\log y_i+(1-t_i)\log (1-y_i) \} \end{align}

この損失関数を交差エントロピー誤差と呼びます。これを最小にするパラメータ$\mathbf{\beta}$を求めます。

交差エントロピー誤差について

交差エントロピー誤差を詳しく見ていきます。

データ$i$の交差エントロピーを$E_i$と書くと、$t_i$は0と1しか取らないことから、以下のように書くことができます。

\begin{align} E_i=\left\{ \begin{array}{l} -\log y_i \qquad\quad &(t_i = 1) \\ -\log(1-y_i) \qquad &(t_i = 0) \end{array} \right. \end{align}

$t_i=0,1$のグラフをそれぞれ書いてみると以下のようになります。

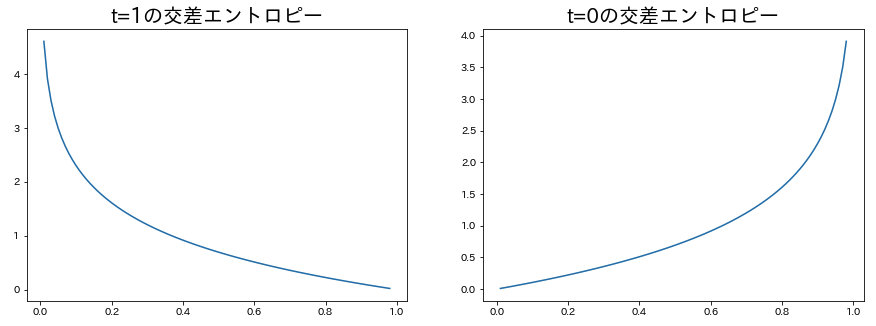
ここから、以下のことがわかります。

$t_i=1$のときは予測確率が1に近いほど損失関数の値が小さい。
$t_i=0$のときは予測確率が0に近いほど損失関数の値が小さい。

損失関数を最小化するということは、上記を目指すことと一致します。

交差エントロピー誤差の最小化

さて、交差エントロピー誤差が最小となるパラメータ$\beta$を求めるため、偏微分していきましょう。

\begin{align} \frac{\partial E}{\partial \beta_k} &= -\sum_{i=1}^n\frac{\partial}{\partial \beta_k}\{t_i\log y_i+(1-t_i)\log (1-y_i)\}\\ \end{align}

シグマの中身の微分を一つずつ処理していきます。

まずは、$\frac{\partial}{\partial \beta_k}\log y_i$を計算します。

$z_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}\cdots\beta_kx_{ik}$とおくと、$y_i=\sigma(z_i)$であり、 $\sigma(x)'=(\frac{1}{1+e^{-x}})'=\frac{e^{-x}}{(1+e^{-x})^2}=\frac{e^{-x}}{1+e^{-x}}\cdot\frac{1}{1+e^{-x}}=(1-\sigma(x))\sigma(x)$ に注意すると、以下のように変形できます。

\begin{align} \frac{\partial}{\partial \beta_k}\log y_i&=\frac{1}{y_i}\frac{\partial y_i}{\partial \beta_k}\\ &=\frac{1}{y_i}\frac{\partial z_i}{\partial \beta_k}\frac{\partial}{\partial z_i}\sigma(z_i)\\ &=\frac{1}{y_i}x_{ik}(1-\sigma(z_i))\sigma(z_i)\\ &=\frac{1}{y_i}x_{ik}(1-y_i)y_i\\ &=(1-y_i)x_{ik} \end{align}

次に、$\frac{\partial}{\partial \beta_k}\log (1-y_i)$を計算します。計算はほぼ上記と同じです。

\begin{align} \frac{\partial}{\partial \beta_k}\log (1-y_i)&=-\frac{1}{1-y_i}\frac{\partial y_i}{\partial \beta_k}\\ &=-\frac{1}{1-y_i}(1-y_i)y_ix_{ik}\\ &=-y_ix_{ik} \end{align}

以上の計算結果を使うと、交差エントロピー誤差の偏微分は以下のようになります。

\begin{align} \frac{\partial E}{\partial \beta_k} &= -\sum_{i=1}^n\frac{\partial}{\partial \beta_i}\{t_i\log y_i+(1-t_i)\log (1-y_i)\}\\ &=-\sum_{i=1}^n\{t_i(1-y_i)x_{ik}+(1-t_i)（-y_ix_{ik}）\}\\ &=-\sum_{i=1}^n(t_i-y_i)x_i = \sum_{i=1}^n(y_i-t_i)x_{ik} \end{align}

とても綺麗な式になりました。

ここから偏微分=0となる$\mathbf{\beta}$を求めたいですが、解析的には解くことができません。

そこで、勾配降下法を用いて$\mathbf{\beta}$を求めます。

勾配降下法は以下の式を使用して$\beta_k$を更新します。$\alpha$は学習率です。

\begin{align} \beta_k \leftarrow \beta_k-\alpha\frac{\partial E}{\partial \beta_k} \end{align}

学習率$\alpha$を入れないで通常の偏微分を引いてしまうと、引く幅が大きくなってしまい、収束しません。従って、$\alpha= 0.01$などを入れて引く幅を小さくします。

また、$\frac{\partial E}{\partial \beta_k} = \sum_{i=1}^n(y_i-t_i)x_{ik}$はデータ数に依存して大きくなってしまうので、実際には代わりにデータ数で割った$\frac{1}{n}\sum_{i=1}^n(y_i-t_i)x_{ik}$を引くことも多いです。 (定数で割ることは更新幅のみに影響するので問題ありません。) 後ほど紹介するコードではデータ数で割った式で更新しています。

パラメータの更新は、交差エントロピー誤差がほとんど動かなくなったら終了です。

なお、厳密には勾配降下法で求めることができるのは極小値です。最小値であることは、損失関数の凸性を示す必要があります。

ここでは証明しませんが、交差エントロピー誤差は凸であることが知られていますので、勾配降下法で最小値を求めることができます。

実際の結果

勾配降下法を用いてロジスティック回帰を回した結果はこのコードを実行してみてください。

まとめ

ロジスティック回帰と最尤推定法に関してまとめました。

交差エントロピー誤差を知っている方は多いかもしれませんが、なぜ交差エントロピーが使用されているかは最尤推定法を学ぶと理解できるかと思います。

最尤推定法は統計的手法のあらゆる箇所で使用されているので、今後も紹介できたらなと思います。